Flächenberechnung

Einheit Bezeichnung Umrechnung

1 mm2
1 cm2
1 dm2
1 m2
1 a
1 ha
1 km2

Quadratmillimeter
Quadratzentimeter
Quadratdezimeter
Quadratmeter
Ar
Hektar
Quadratkilometer

-
1 cm2 = 100 mm2
1 dm2 = 100 cm2 = 10000 mm2
1 m2 = 100 dm2 = 10000 cm2
1 a = 100 m2
1 ha = 100 a2
1 km2 = 100 ha = 1000 m ·1000 m2

Die Umwandlungszahl für Flächen ist 100: 1 m2 = 100 dm2. 1 dm2 = 100 cm2. 1 cm2 = 100 mm2

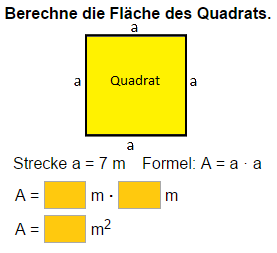
Die Fläche eines Quadrats berechnen.
Die Eigenschaften eines Quadrats.

Alle Seiten des Quadrats sind gleich lang.
Alle Winkel des Quadrats sind 90 Grad.
Die Diagonalen des Quadrats sind gleich lang.
Die Diagonalen des Quadrats halbieren sich.
Die Diagonalen des Quadrats stehen senkrecht aufeinander.

Berechnung: Flächeninhalt eines Quadrats: A = a · a

So berechnest du den Flächeninhalt eines Quadrats
Seitenlänge a = 5 cm

Formel: A = a · a
Berechnung A = 5 cm · 5 cm
Ergebnis: A = 25 cm2

Die Eigenschaften des Rechtecks

Die Fläche eines Rechtecks berechnen.
Eigenschaften des Rechtecks

Merke:
Gegenüber liegende Seiten des Rechtecks sind gleich lang.
Alle sich gegenüber liegenden Seiten des Rechtecks sind parallel.
Alle Winkel des Rechtecks sind 90 Grad.
Die Diagonalen des Rechtecks sind gleich lang.
Die Diagonalen des Rechtecks halbieren sich.

Berechnung Flächeninhalt eines Rechtecks: A = a · b

So berechnest du den Flächeninhalt eines Rechtecks
Seitenlänge a = 3 cm, Seitenlänge b = 5 cm

Formel: A = a · b
Berechnung A = 3 cm · 5 cm
Ergebnis: A = 15 cm2

Hier kannst du die Längenmaße wiederholen.

Flächen berechnen: Übungen

Übunge für die Berechnung von Flächen in Klasse 5.
Übungen für die Berechnung von mm, cm und m starten.

Erklärungen und Beispiele zur Flächenberechnung

Aufgaben zur Umrechnung von Quadratmillimeter (mm2), Quadratzentimeter (cm2), Quadratdezimeter (dm2), Quadratmeter (m2), Ar (a) Hektar (ha), Quadratkilometer (km2) mit Online-Übungen, Lösungen und Erklärungen. Die Flächenberechnung für Quadrat und Rechteck. Mathematik Flächenberechnung - Übungen für Realschule, Gymnasium, Gesamtschule und Oberschule für Klasse 4, Klasse 5 und Klasse 6.

Übungen für die schriftliche Addition Klasse 3, Klasse 4 und Klasse 5.