Ungleichnamige Brüche - Addition Subtraktion
Die Addition bei ungleichnamigen Brüchen.
Brüche sind ungleichnamig, wenn sie nicht den gleichen Nenner
haben. Dies ist bei dem folgenden Beispiel so. Der Nenner besteht aus Viertel
und Halben.
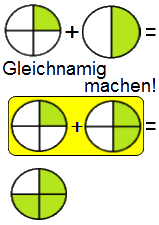 |
Ungleichnamige Brüche addiert man, indem man zuerst den Nenner gleichnamig
macht. Danach kann man Zähler plus Zähler addieren.
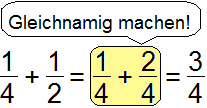
Wie macht man einen Nenner gleichnamig, um zu addieren?
Man sucht eine Zahl, durch die man alle Zahlen des Nenners teilen kann. Wer das
kleine 1x1 auswendig kann, für den ist dies einfach.
 |
Die Subtraktion bei ungleichnamigen Brüchen.
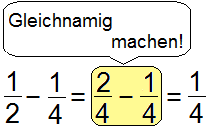
Ungleichnamige Brüche subtrahiert man, indem man zuerst den Nenner gleichnamig
macht. Danach kann man Zähler minus Zähler subtrahieren.
Wie macht man einen Nenner gleichnamig, um zu subtrahieren?
Man sucht eine Zahl, durch die man alle Zahlen des Nenners teilen kann.
 |
Gemischte Zahl: Eine gemischte Zahl besteht aus einer ganzen Zahl und einem Bruch. Beispiel:
| 2 | |
Unechter Bruch: Bei einem unechten Bruch ist der Zähler größer ist als der Nenner. Beispiel:
Wenn man ein Ganzes als Bruch schreibt, sind Zähler und Nenner gleich.
Einen Bruch kann man erweitern, wenn man Zähler und Nenner des Bruches mit der
gleich Zahl
multipliziert. Im folgenden Beispiel wird der Bruch mit 2 erweitert. Die
Multiplikation von Zähler und Nenner mit 2 macht aus ein Halb schließlich zwei
Viertel.
Beispiel für das Erweitern eines Bruches:
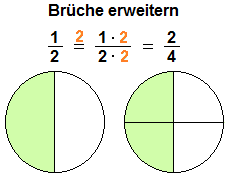 |
Durch das Erweitern des Bruches entsteht wieder ein Bruch. Bei dem Kreis im
obigen Beispiel bleibt die grüne Fläche gleich, sie wird beim Erweitern des
Bruches nur feiner aufgeteilt.
Ein Beispiel für das Erweitern eines Bruches von ein Halb auf drei Sechstel:
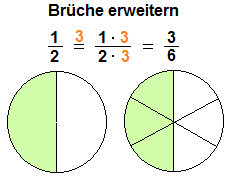 |
Noch ein Beispiel für das Erweitern eines Bruches von ein Halb auf vier Achtel. Zähler und Nenner werden beide mit 4 multipliziert und damit erweitert. Das Ergebnis der Erweiterung ist vier Achtel.
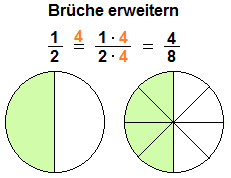 |
Ein Beispiel für das Erweitern eines Bruches von ein Halb auf fünf Zehntel. Zähler und Nenner müssen mit 5 erweitert werden, um das Ergebnis fünf Zehntel zu erhalten. Mit dem Erweitern ist wieder ein Bruch entstanden.
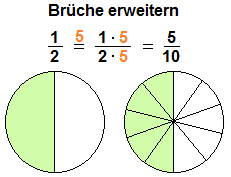 |
Addieren und Subtrahieren von ungleichnamigen Brüchen
Ungleichnamige Brüche mit Erklärungen und Übungen. Zähler und Nenner zur Berechnung von ungleichnamigen Brüchen, ungleichnamige Brüche berechnen und umwandeln mit online Übungen. Mathematik Übungen für Realschule, Gymnasium, Gesamtschule und Oberschule für Klasse 5 und Klasse 6.
nächste Übung